水波球进度

好几年前的一个 h5 项目视觉中需要类似一个装有水的球，通过水位线来表示进度。当时因种种原因没有做了，最终是纯靠视觉切图分阶段表现的。也一直想自己试着画一下，最近正好有个契机给实现了一下，本文就大概说一下实现思路。

一个小玩意，类似下图，当然本文实现没这么炫了。实际不难，重在思路。

基本实现方式

首先将上面的视觉稿抽象，去掉视觉贴图内容，主要有两个部分：

球的外框：这个简单的可以直接画一个圆，想带点效果就用材质或直接贴图；
球内的水：也是主要实现的重点，实现方法也不只是一种，本文讲两种方式：
- dom 实现方法，(也可以用 canvas 实现，只是用 dom 更简单直接)
- 纯 canvas 绘制方法

dom 方法

这个方法比较简单，由一个带 overflow: hidden; 的圆形 div 做容器，里面放一个足够大的(至少和容器一样大)的“水”的矩形贴图，就可以轻松实现了。

<div class="container">
  <div class="water"></div>
</div>

.container {
	position: absolute;
	width: 200px;
	height: 200px;
	left: 0;
	top: 0;
	border-radius: 50%;
	overflow: hidden;
}
.water {
	width: 100%;
	height: 100%;
	margin-top: 10%; // 这里直接控制水位
	background: transparent url('/src/css/img/water.png') no-repeat center top;
	background-size: 150%;
}

水位占到球的百分之多少，只需要控制 .water 的 margin-top 即可。

补充一个这个方法的 canvas 实现： canvas 里默认没有类似 overflow: hidden; 这样的属性，所以需要借助一些绘图库，如 PIXIJS，里面有 mask 这样的有限绘制区域遮罩，设置一个图形的 mask，用同样的原理，也很方便实现。

canvas 绘制

这个方法相对麻烦一些，需要进行一些简单的数学建模和计算。整体上把这水位的部分分成两次曲线绘制：

用 drewCircle 方法画一个扇形的圆弧
再在圆弧上面开口的部分用一个模拟水面的曲线闭合，本文使用 bezierCurveTo 方法

加上搭边和颜色填充，就能实现这个图形。

几何分析

主要的部分就是按绘制模型的需要，算出各个关键点的坐标：

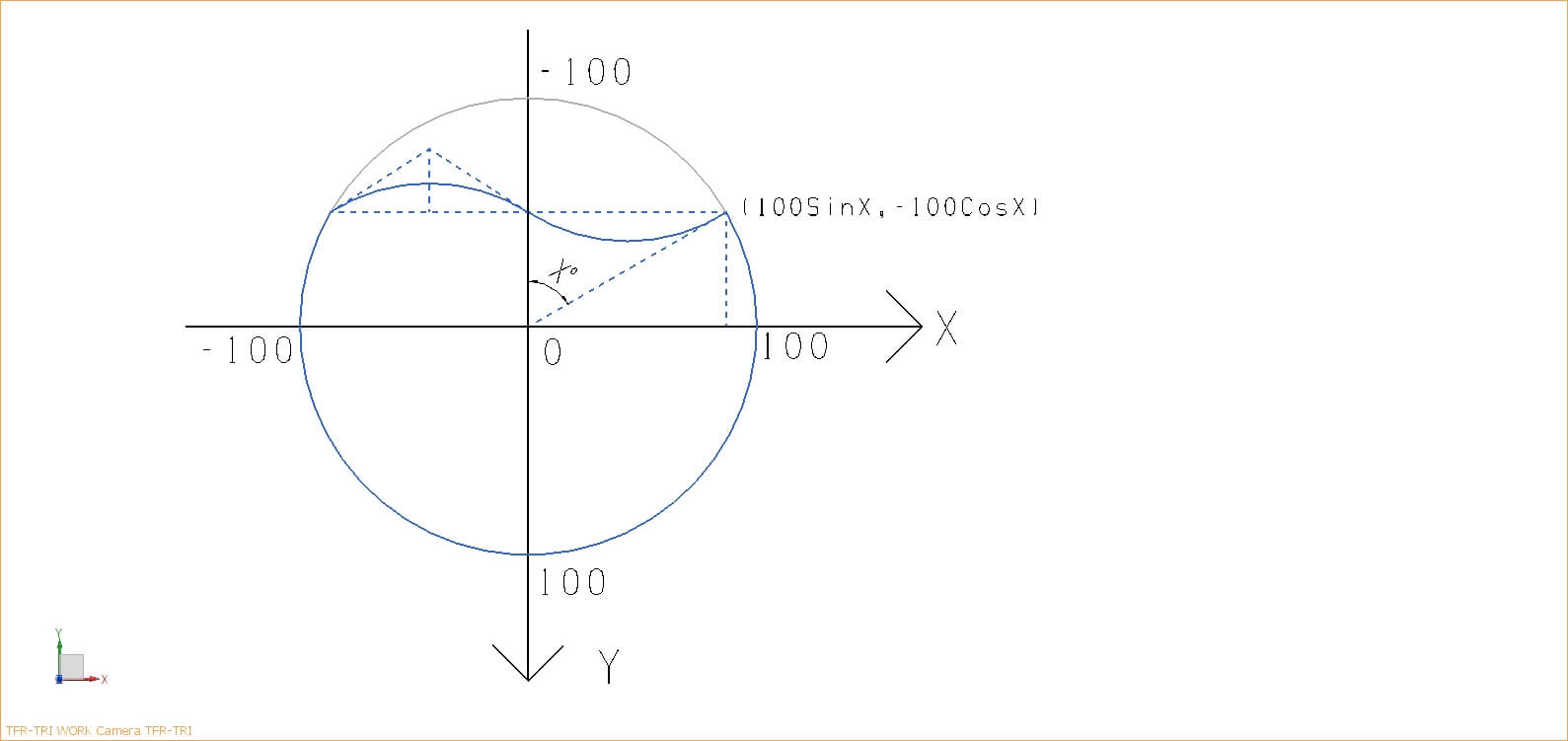
以这个圆的中心为原点建立坐标系。假设球的半径是 radius = 100，水位占球的比例是 p：

图上 x 角的度数 degOfPI，顺带把 sinx 也得出来，后面会用到：

const cosx = (radius * 2 * p - radius) / radius;
const sinx = Math.sqrt(1 - Math.pow(cosx, 2));
const degOfPI = Math.acos(cosx);

算出绘制扇形的起始角和结束角：

const startDeg = 0 - (Math.PI / 2 - degOfPI);
const endDeg = Math.PI + (Math.PI / 2 - degOfPI);

定扇形的右上点为起始点，先算出 x、y 的坐标偏移量：

const _x = radius * sinx;
const _y = radius * cosx;

这里注意需要注意两点：

理论上 _x 肯定是正值，_y 有正有负(当水位比例 p < 50% 的时候);
但右上角起始点的坐标并不是 (_x, _y)，因为一般 canvas 中的坐标 y 轴方向和几何坐标的 y 轴方向是反的，所以起始点的坐标是 (_x, -_y)。

现在开始画扇形：

// Graphics 伪代码实现 eg：
const graphics = new Graphics();
graphics.arc(0, 0, radius, startDeg, endDeg, false);

画完扇形后，笔触正好到左边，然后继续画一条水面曲线就搞定了，这里用的 bezierCurveTo 方法怎么使用和原理就不再赘述了，可以自行查文档。

结束点和起始点的 x 坐标是对称的，选取左右两边矩 y 轴的距离的中心为两个贝塞尔控制点的 x 坐标，自行选择上下偏移 l 距离分别作为这两个控制点的 y 坐标，最终回到起始点 (_x, -_y)。这样就大功告成了。

graphics.bezierCurveTo(
  -(_x / 2), -_y + l,
  _x / 2, -_y - l,
  _x, -_y
);

示例代码

const radius = 球半径;
const p = 水位线比例;
const cosx = (radius * 2 * p - radius) / radius;
const sinx = Math.sqrt(1 - Math.pow(cosx, 2));
const degOfPI = Math.acos(cosx);
// 
const startDeg = 0 - (Math.PI / 2 - degOfPI);
const endDeg = Math.PI + (Math.PI / 2 - degOfPI);
const _x = radius * sinx;
const _y = radius * cosx;
const l = 20; // 贝塞尔上下波动距离
//
const graphics = new Graphics();
graphics.lineStyle(0);
graphics.beginFill(0xffffff, 0.5);
graphics.arc(0, 0, radius, startDeg, endDeg, false);
graphics.bezierCurveTo(
  -(_x / 2), -_y + l,
  _x / 2, -_y - l,
  _x, -_y
);
graphics.endFill();
// 补上一个外框
graphics.moveTo(radius + 8, 0);
graphics.lineStyle(4, 0xffffff, 1);
graphics.arc(0, 0, radius + 8, 0, 2 * Math.PI, false);
graphics.endFill();

效果

最终效果如上图，只是很简单的效果，实际中可在此基础上添加视觉效果或动效等。一般方法一就足够用了，实现简单，性能也好。第二种可以做为借鉴，在类似的必须要绘制的场景来参考。

Yinjie - GitHub.io